调节效应分析（ Moderation Analysis ），回答 WHEN 的问题

之前整理了中介效应分析，解决了怎么看中介效应是否显著的问题。

这篇继续整理调节效应分析（Moderation Analysis）

中介变量回答的是关于 HOW 的问题，而调节变量回答的是关于 WHEN 的问题

$X$ 什么时候影响 $Y$，或 $X$ 影响 $Y$ 的过程中是否取决于变量 $W$ ，而变量 $W$ 就是调节变量

典型且简单的调节效应模型图如下所示

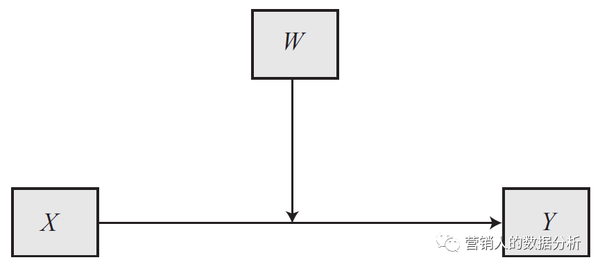
理论先行

调节效应理论模型用 statistical diagram 表示为，

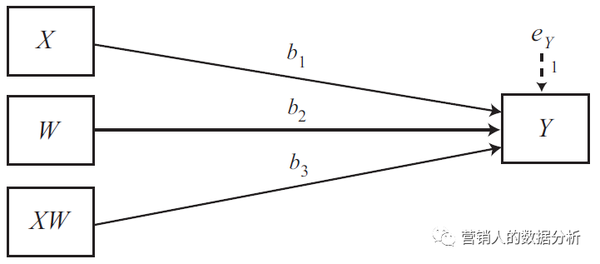
即，

$$ Y=i_Y+b_1X+b_2W+b_3XW+e_Y $$

系数解释

各系数的解释如下

$b_1$

$b_1$ 是当 $W=0$ 时，$X$ 改变一个单位，$Y$ 改变 $b_1$

$$ b_1=[\widehat{Y}|(X=x+1,W=0)] - [\widehat{Y}|(X=x,W=0)] $$

$b_2$

$b_2$ 是当 $X=0$ 时时，$W$ 和 $Y$ 之间的关系

$$ b_2=[\widehat{Y}|(W=w+1,X=0)] - [\widehat{Y}|(W=w,X=0)] $$

$b_3$

这是个大头，他是比较两组之间的差异，

一组是 $W$ 不变，$X$ 改变一个单位

另一组是，$W$ 和 $X$ 都改变一个单位

即，

$$ b_3=([\widehat{Y}|(X=x+1,W=w)] - [\widehat{Y}|(X=x,W=w)]) - ([\widehat{Y}|(X=x+1,W=w+1)] - [\widehat{Y}|(X=x,W=w)]) $$

做调节效应分析的时候， 理论上是希望 $X$ 影响 $Y$ 的过程中取决于变量 $W$

对应着，公式（1）也可以改写为，

$$ Y=i_Y+ \theta_{X \rightarrow Y}X + b_2W + e_Y $$

其中，$\theta_{X \rightarrow Y} = b_1+b_3W$

这也就生动形象的表示了，

如果 $b_3$ 显著性不等于 0 ，那么 $W$ 的值不同，$X$ 对 $Y$ 的影响也不同

所以当回归结果中，系数 $b_3$ 显著时（$p<0.05$），即变量 $W$ 的确起到调节作用时

我们将会进一步分析对应不同 $W$，$X$ 是如何影响 $Y$ 的

常用的方法便是 pick-a-point approach ，又称 spotlight analysis

我第一次看到 spotlight analysis 这个名词，是在一篇JM的文章上，当时查了半天也不知道啥意思。。。

pick-a-point approach

基本思路是根据 $W$ 的数据选三个值，进而表示低-中-高三种状态

一般就选数据16th, 50th, and 84th分位数分别表示低-中-高，进而分析 $X$ 对 $Y$ 的影响是否显著

如果 $W$ 是分类变量就直接看各自类别的情况了，不用取点了。

所以，综上所述，基于公式(1) 构建回归模型，根据交互项系数 $XW$（$b_3$）是否显著，进而确定调节效应是否存在。

以上这些都能通过PROCESS¹很好的实现。

实际操作

步骤如下：

1. SPSS加载 process的语法文件

使用过程中可以自主编写语法、也可以菜单式的操作，如

process y=justify/x=frame/w=skeptic/model=1/plot=1.

2. 变量和数据字段一一对应

3. 基于理论研究模型，选择PROCESS的模型（本例对应的是model 1）

4. 选项中勾选 Generate code for visualizing interactions

如果是用spss语法的话，加上 plot=1 即可

这能方便用SPSS作斜率图，用于可视化调节效应

复制PROCESS分析结果中的可视化脚本即可，如

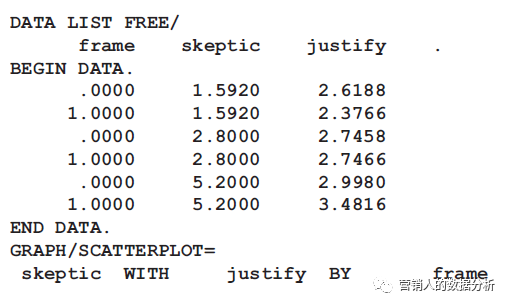
5. （可选）中心化

有些文章中会说做调节效应分析前，对变量 $X$ 和 $Y$ 进行中心化处理，可能会见到 scaling 这样的术语

但其实无所谓啦，而且就算对和进行中心化处理，也不会影响 $W$、$XW$ 的系数，只是会影响 $X$ 的系数（$b_1$）罢了

因为之前有提到，$b_1$ 是表示 $W$ 为0时，$X$ 对 $Y$ 的影响，如果对 $W$ 做中心化处理，

即 $W^,=W - \overline{W}$

那么这时候 $X$ 的系数对应的是 $W$ 取样本均值（$\overline{W}$）时，$X$ 对 $Y$ 的影响

得到结果之后，直奔交互项系数（本例对应的是 $b_3$）即可

若显著（$p<0.05$），PROCESS便会生成低-中-高状态下，$X$ 和 $Y$ 之间的关系如下所示，

参考资料