常见的还款方式:等额本息、等额本金、等本等息
一个一个来盘
等额本息
基本信息
等额本息还款法,也称定期付息。借款人每月按相等的金额偿还贷款本息,其中每月贷款利息按月初剩余贷款本金计算并逐月结清。(MBA智库百科)
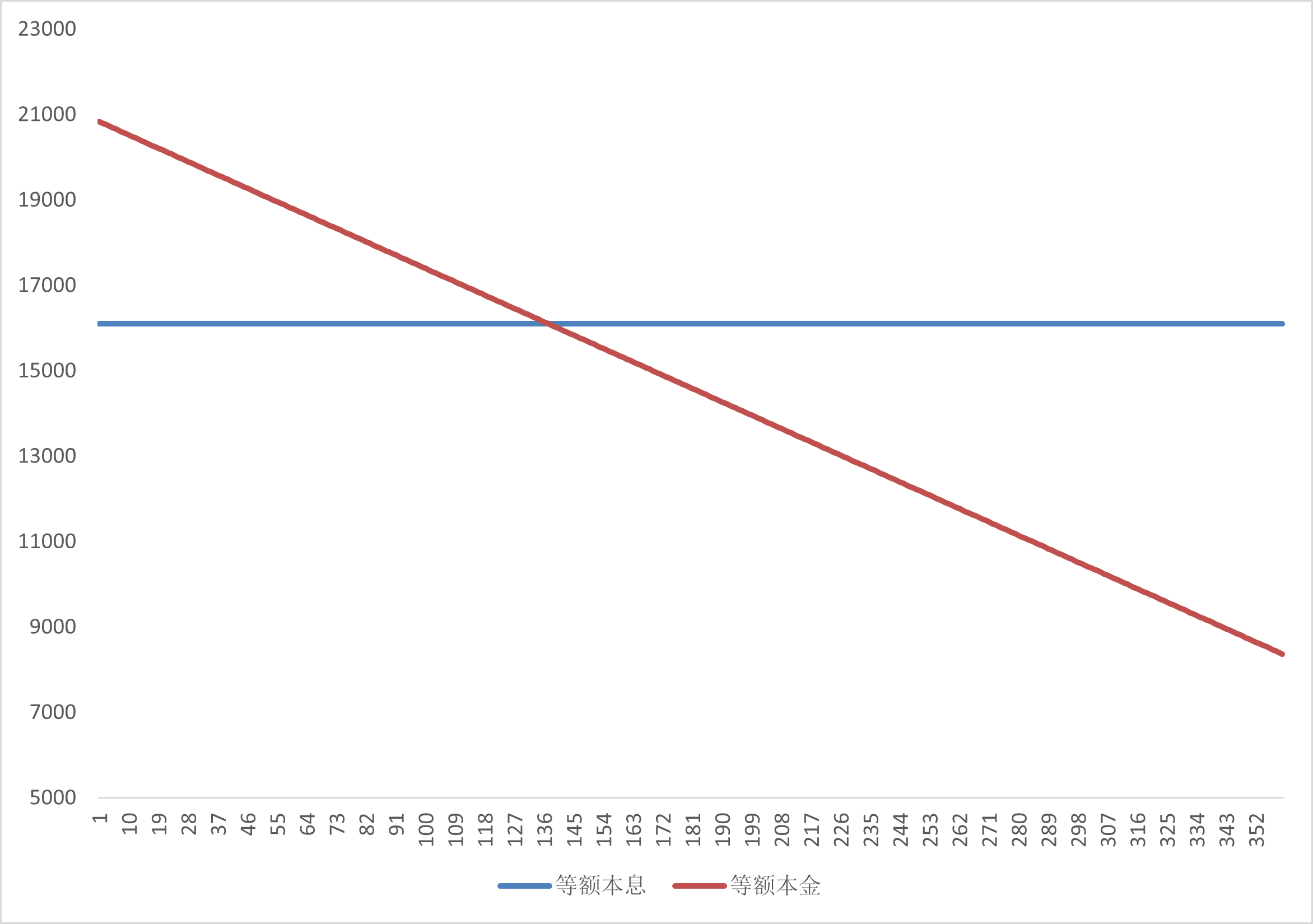
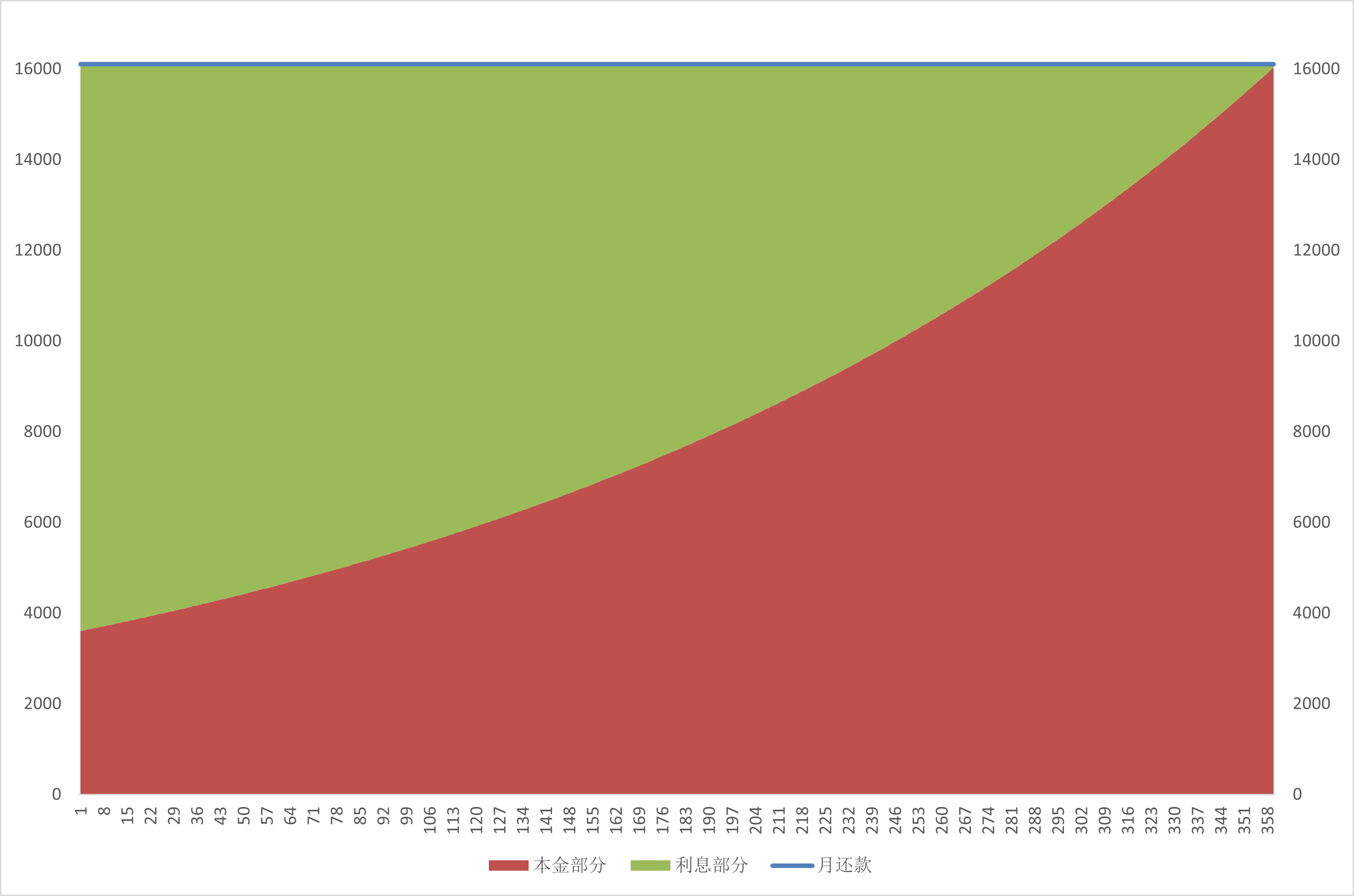
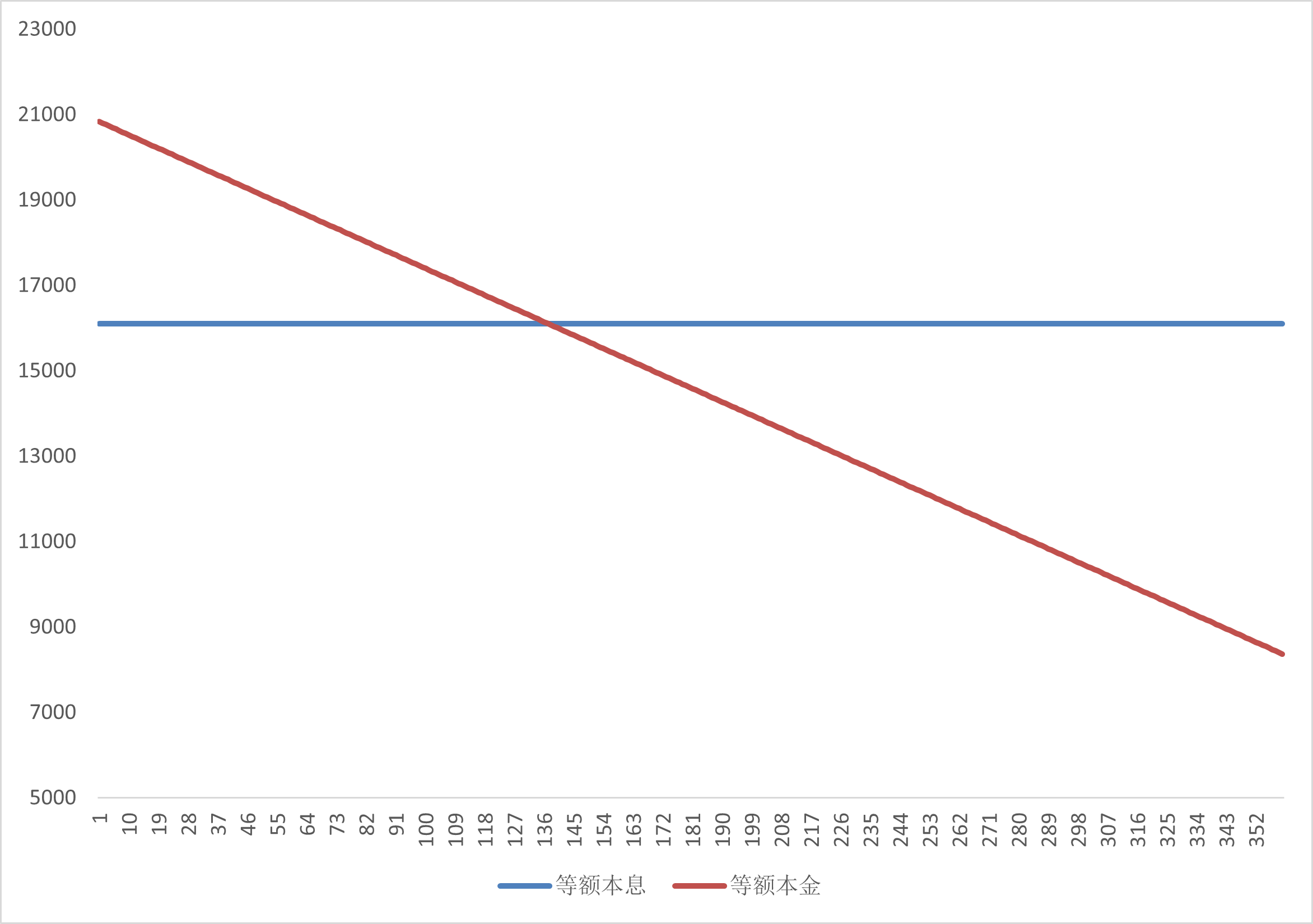
每期还的钱是固定的,即每期 本金+利息 总额是固定的。但每期还的钱中 本金、利息 的占比是动态的 👇

上图中基本信息,假设
- 借款总额:300w
- 借款年限:30
- 年利率:5%
具体公式
假设借款总额 $p$ 元,分了 $n$ 期,每期的利率是 $r$,那么
$$
每期应还款=\frac{p \times r \times (1+r)^n}{(1+r)^n-1}
$$
$$
第i期还款中本金部分=p \times r \times \frac{(1+r)^{(i-1)}}{(1+r)^n-1}
$$
$$
第i期还款中利息部分=\frac{p \times r}{(1+r)^n-1} \times ((1+r)^n-(1+r)^{(i-1)})
$$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
|
import pandas as pd
class MRPI:
'''
等额本息
- 多种翻译
Matching the Repayment of Principal and interest
/ Fixed installment method
/ average capital plus interest method
计算
- 每月还款
- 本金、利息部分
- generate DataFrame
'''
def __init__(self, p,R,N):
'''
p: 贷款总额
R: 年化利率
N: 贷款年限
'''
self.p = p
self.R = R
self.N = N
self.n = N * 12
self.r = R / 12
def pay_amt(self):
'''
每期总额(月供)
'''
term_total = ( self.p * self.r * (1 + self.r)**self.n ) \
/ ( (1 + self.r)**self.n - 1 )
return round(term_total,2)
def pay_part(self):
'''
月供中 利息,本金 部分
'''
interest,principal = [],[]
for i in range(self.n):
# 利息
term_interest = self.p * self.r * ( (1+self.r)**self.n - (1+self.r)**i ) \
/ ((1+self.r)**self.n-1)
term_interest = round(term_interest,2)
interest.append(term_interest)
# 本金
term_principal = ( self.p * self.r * ( 1 + self.r )**i ) \
/ ( (1 + self.r)**self.n - 1 )
term_principal = round(term_principal,2)
principal.append(term_principal)
return interest,principal
def get_detail(self):
'''
convert to DataFrame
'''
df_detail = pd.DataFrame({"term":[i for i in range(1,self.n + 1)]
,"月还款":[self.pay_amt()]*self.n
,"本金部分":self.pay_part()[1]
,"利息部分":self.pay_part()[0]
})
df_total = pd.DataFrame({"term":["总计"]
,"月还款":[self.pay_amt()*self.n]
,"本金部分":[self.p]
,"利息部分":[self.pay_amt()*self.n - self.p]
})
df = df_detail.append(df_total)
return df_detail,df.reset_index(drop=True)
|
等额本金
等额本金还款法,也称利随本清、等本不等息还款法。借款人将本金分摊到每期,同时付清上一个交易日至本次还款日之间的利息。(MBA智库百科)
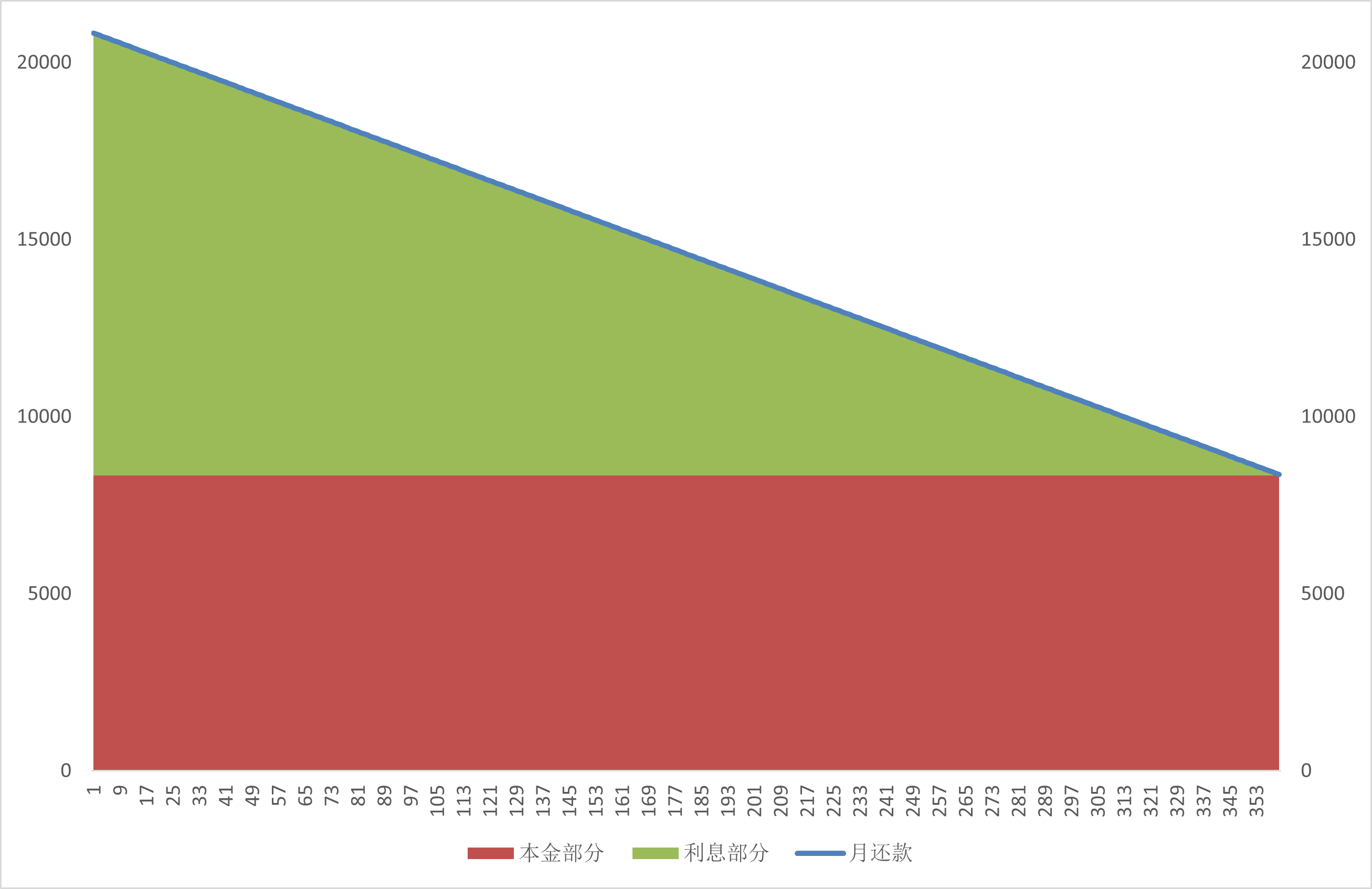
每期还的本金是固定的,随着剩余本金的减少,利息便也动态减少 👇 但前期还款总额较多

上图中基本信息,假设
- 借款总额:300w
- 借款年限:30
- 年利率:5%
具体公式
$$
第i期应还款=\frac{p}{n} + (1- \frac{i-1}{n}) \times p \times r
$$
$$
第i期还款中本金部分=\frac{p}{n}
$$
$$
第i期还款中利息部分=(1- \frac{i-1}{n}) \times p \times r
$$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
|
import pandas as pd
class MPR:
'''
等额本金
- 多种翻译
Matching the Principal Repayment
/ Reducing installment method (Fixed Principal)
/ average capital method
计算
- 每月还款
- 本金、利息部分
- generate DataFrame
'''
def __init__(self, p,R,N):
'''
p: 贷款总额
R: 年化利率
N: 贷款年限
'''
self.p = p
self.R = R
self.N = N
self.n = N * 12
self.r = R / 12
def pay_part(self):
'''
本金,每期总额(月供) 以及 利息部分
'''
# 本金
term_principal = self.p / self.n
amt,interest = [],[]
for i in range(self.n):
# 每期利息
term_interest = ( 1 - i/self.n ) * self.p * self.r
# 每期还款
term_amt = term_principal + term_interest
term_amt = round(term_amt,2)
amt.append(term_amt)
term_interest = round(term_interest,2)
interest.append(term_interest)
return round(term_principal,2),amt,interest
def get_detail(self):
'''
convert to DataFrame
'''
df_detail = pd.DataFrame({"term":[i for i in range(1,self.n + 1)]
,"月还款":self.pay_part()[1]
,"本金部分":[self.pay_part()[0]]* self.n
,"利息部分":self.pay_part()[2]
})
df_total = pd.DataFrame({"term":["总计"]
,"月还款":[self.p + (self.n+1)*self.p*(self.r/2)]
,"本金部分":[self.p]
,"利息部分":[self.p*(self.n+1)*(self.r/2)]
})
df = df_detail.append(df_total)
return df_detail,df.reset_index(drop=True)
|
俩还款方式每期还款金额如下图所示

等本等息
关于这个“等本等息”,常见于互金的现金贷业务、信用卡分期等
上面的等额本息、等额本金还款方式在计算每一期的利息时,也有按照占用借款时间的概念来计算,即还了的部分就不计算利息了
但 “等本等息”还款方式一开始就计算的死死的,每期还款中本金、利息都是固定的
比如,小明借了12w元,年利率是12%,分12期还。那么每期应还$11200=(\frac{120000*(1+0.12)}{12})$
还是基于 12w,年利率12%,分12期的情况,不同还款方式的情况如下所示
|
等额本金 |
等额本息 |
等本等息 |
| 1 |
11200 |
10661.85 |
11200 |
| 2 |
11100 |
10661.85 |
11200 |
| 3 |
11000 |
10661.85 |
11200 |
| 4 |
10900 |
10661.85 |
11200 |
| 5 |
10800 |
10661.85 |
11200 |
| 6 |
10700 |
10661.85 |
11200 |
| 7 |
10600 |
10661.85 |
11200 |
| 8 |
10500 |
10661.85 |
11200 |
| 9 |
10400 |
10661.85 |
11200 |
| 10 |
10300 |
10661.85 |
11200 |
| 11 |
10200 |
10661.85 |
11200 |
| 12 |
10100 |
10661.85 |
11200 |
| 总计 |
127800 |
127942.2 |
134400 |
总结
本文罗列了等额本息、等额本金和等本等息三种还款方式的基本信息。但产品设计的角度思考较少
虽然表面上看起来等本等息还款方式很暴力,但我觉得每种还款方式背后都有金融产品设计者的考虑吧
银行不会雪中送炭,只会锦上添花。小额贷款等机构 、平台都是一样的,在风险可承受的情况下给予放款,毕竟这是门生意
但政府的监管,限制利率上限等政策,带来的结果便是,更多的人借不到钱 🤷♂️
原本的毛细血管更加的“细”。
从奥派的角度来看“高利贷”等问题,可参考陈志武教授的这篇文章
 胡子叔叔的小站
胡子叔叔的小站