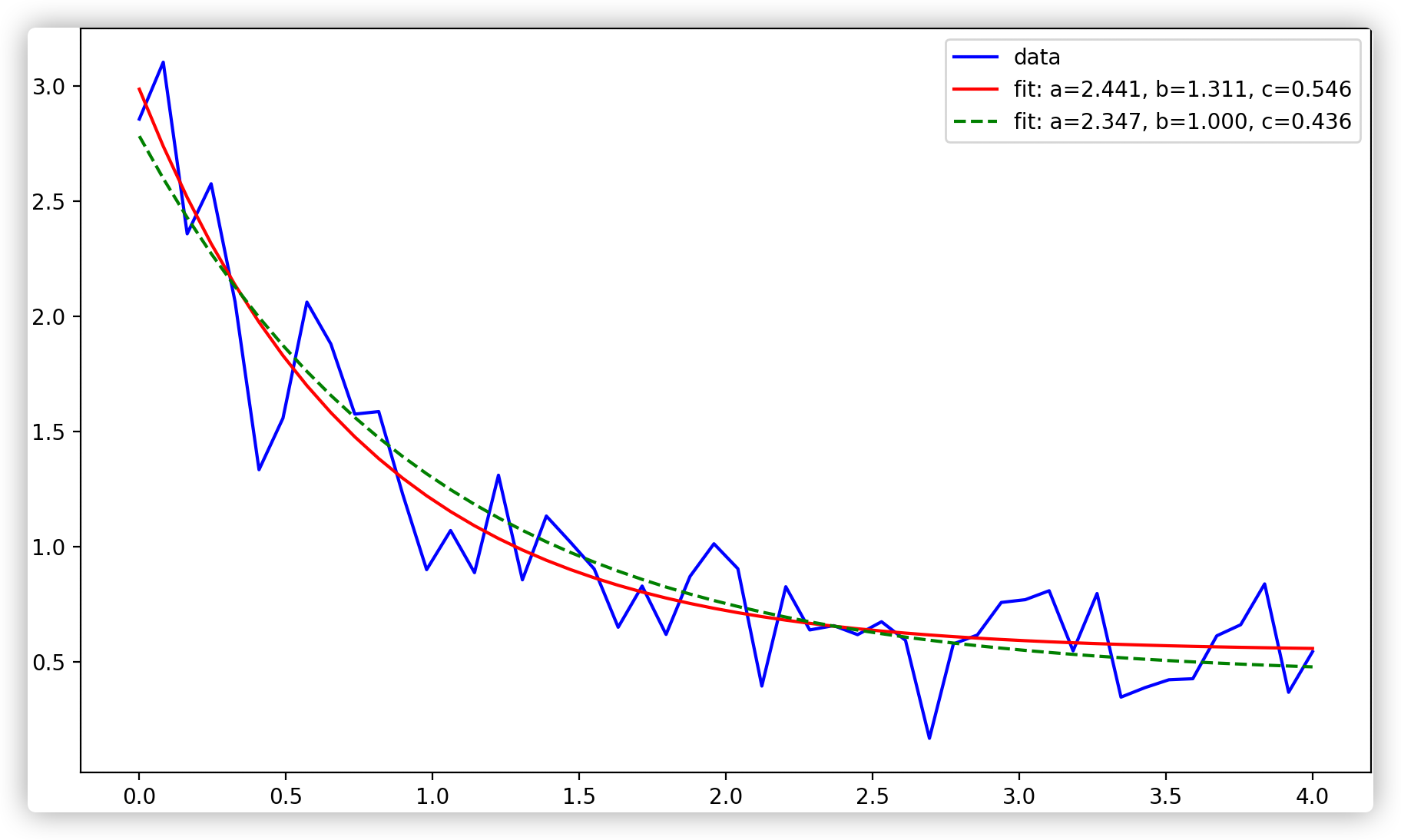
Python曲线拟合
curve fitting
最近接触了曲线拟合(curve fitting),在此简单整理一波Python的实现方式
依稀记得高中数学课本有提到这个,$x$、$y$ 二维坐标。大致是两种方式:一种是看着像啥样或基于先验知识给出常见函数的关系式,通过数据拟合得到相应的系数;第二种是直接从数据出发,采用“基函数”拟合,和泰勒展开、级数有关系,函数越复杂拟合的越完美,但泛化能力就有待考究了,即复杂度越高越容易出现过拟合
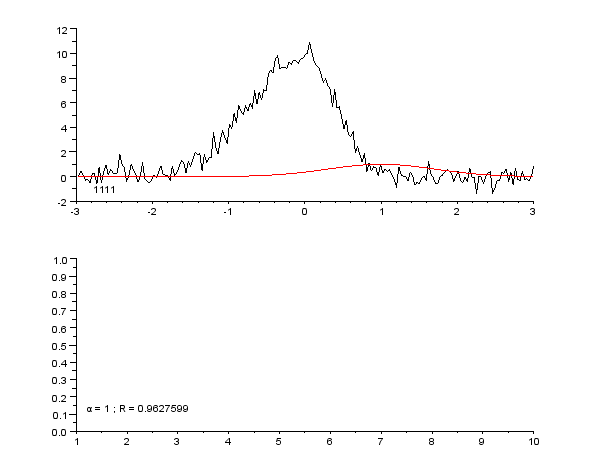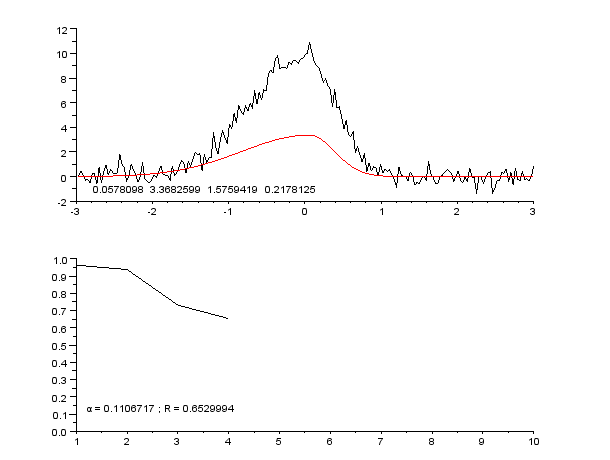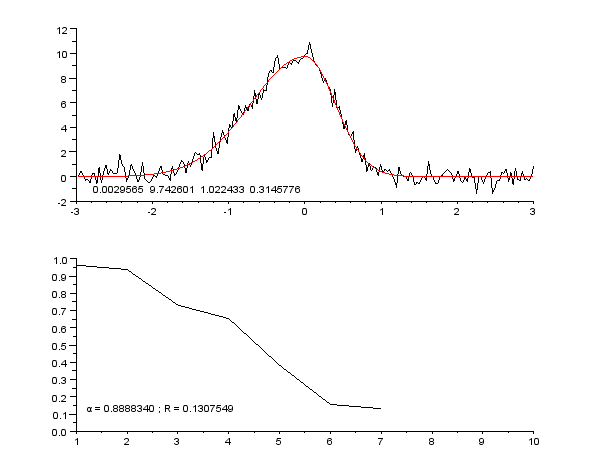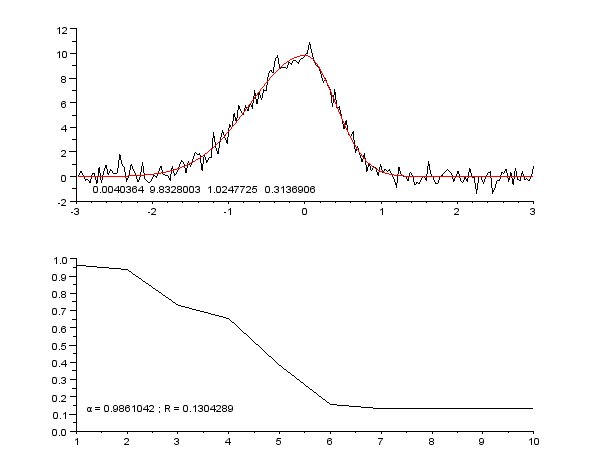
「插播」这两种又让我想起了统计里的“参数估计”和“非参数估计”
备注:以下分类名称仅从个人理解出发
自定义函数拟合
“自定义函数拟合”即我们可以自行编写定义各种函数(如幂函数、指数函数等)关系,基于此对现有数据进行拟合。往往需要一些领域内的知识🤔
具体实现可参考 scipy.optimize.curve_fit
官方示例
|
|
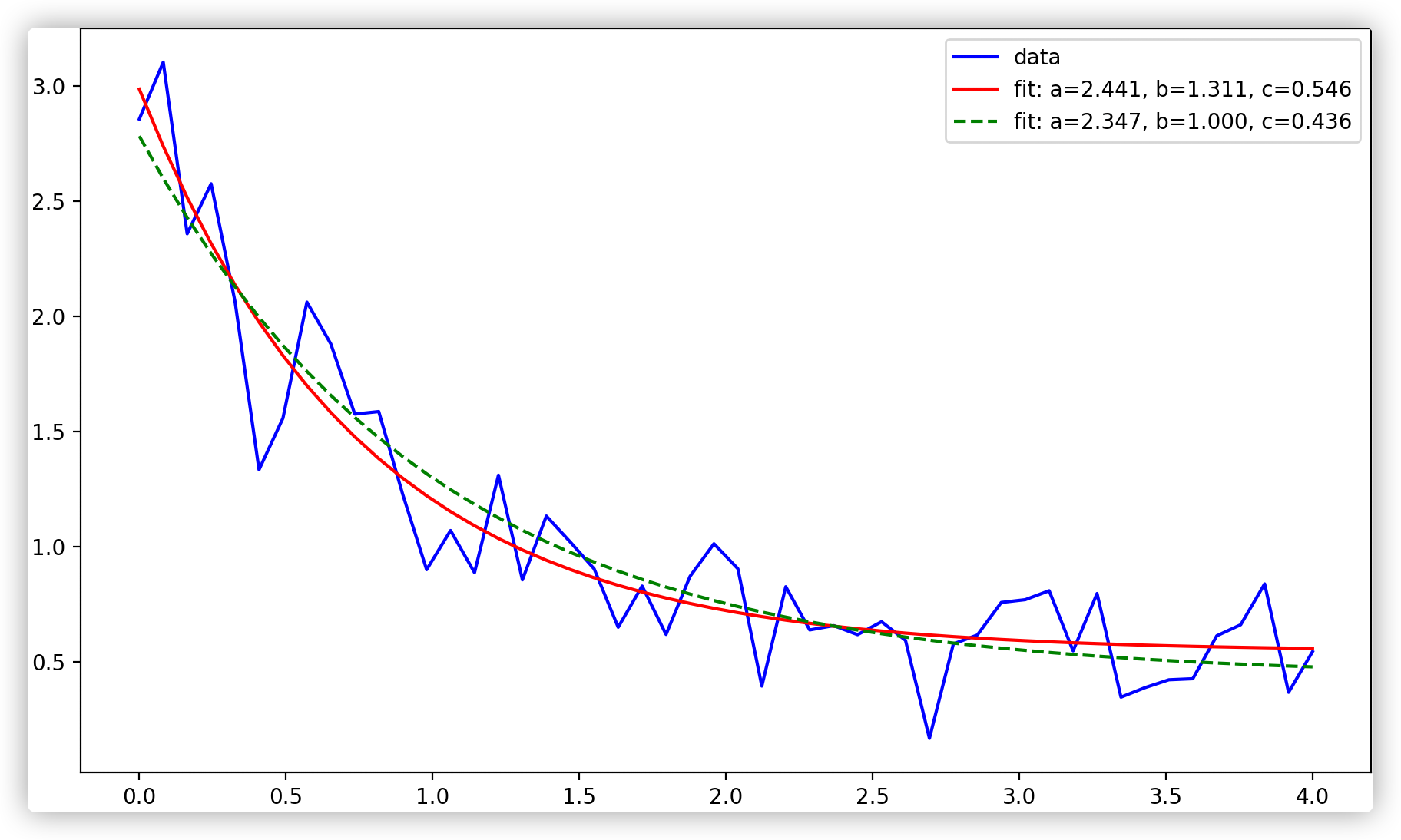
curve_fit() 的参数方面:
-
p0系数初始值
-
bounds各系数的取值范围
-
method最优化算法,’lm’, ’trf’, ‘dogbox’
MARK-log
此外还要 MARK 的一点是关于 $log$ 的问题,Python中 numpy 和 math 都可以计算对数($log$)
首先 math.log 和 numpy.log 都是以自然常数 $e$ 为底的自然对数,针对底数不同各自都有以2、10为底的函数,分别为log2(), log10() 。其中,math.log2(x), math.log10(x)计算的准确性高于 math.log(x,2), math.log(x,10)
但是 math.log() 支持自选底数,比如计算 $log_{12}{10}$ :math.log(10,12)
其实结合“换底公式”, 这个就等价于 math.log(10)/math.log(12)
$$
log_ab=\frac{log_ca}{log_cb}
$$
但但但但是,numpy.log 是支持数组、列表等形式的,享受 broadcasting带来的快感;而 math.log 只支持单个数字的计算,若传入数组等 array_like 则会报错:TypeError: only size-1 arrays can be converted to Python scalars
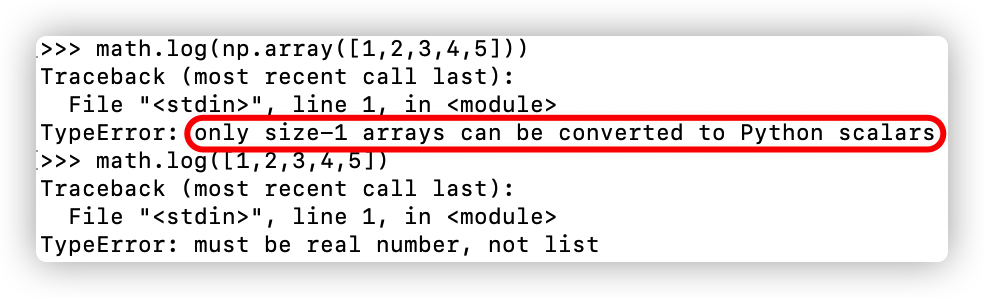
若一定要用 math.log 也是可以的: [math.log(i) for i in [1,2,3,4,5]]

基函数拟合
关于这部分,目前记录的 “基函数” 更多是多项式(polynomials)形式,numpy提供了 sub-package: numpy.polynomial (NumPy 1.4 版本,2009-12-28,引入的)
| Name | Provides |
|---|---|
Polynomial |
Power series |
Chebyshev |
Chebyshev series |
Legendre |
Legendre series |
Laguerre |
Laguerre series |
Hermite |
Hermite series |
HermiteE |
HermiteE series |
Power series(Polynomial)就是我们常见的 $y=1+2x+3x^2$ 这种
|
|
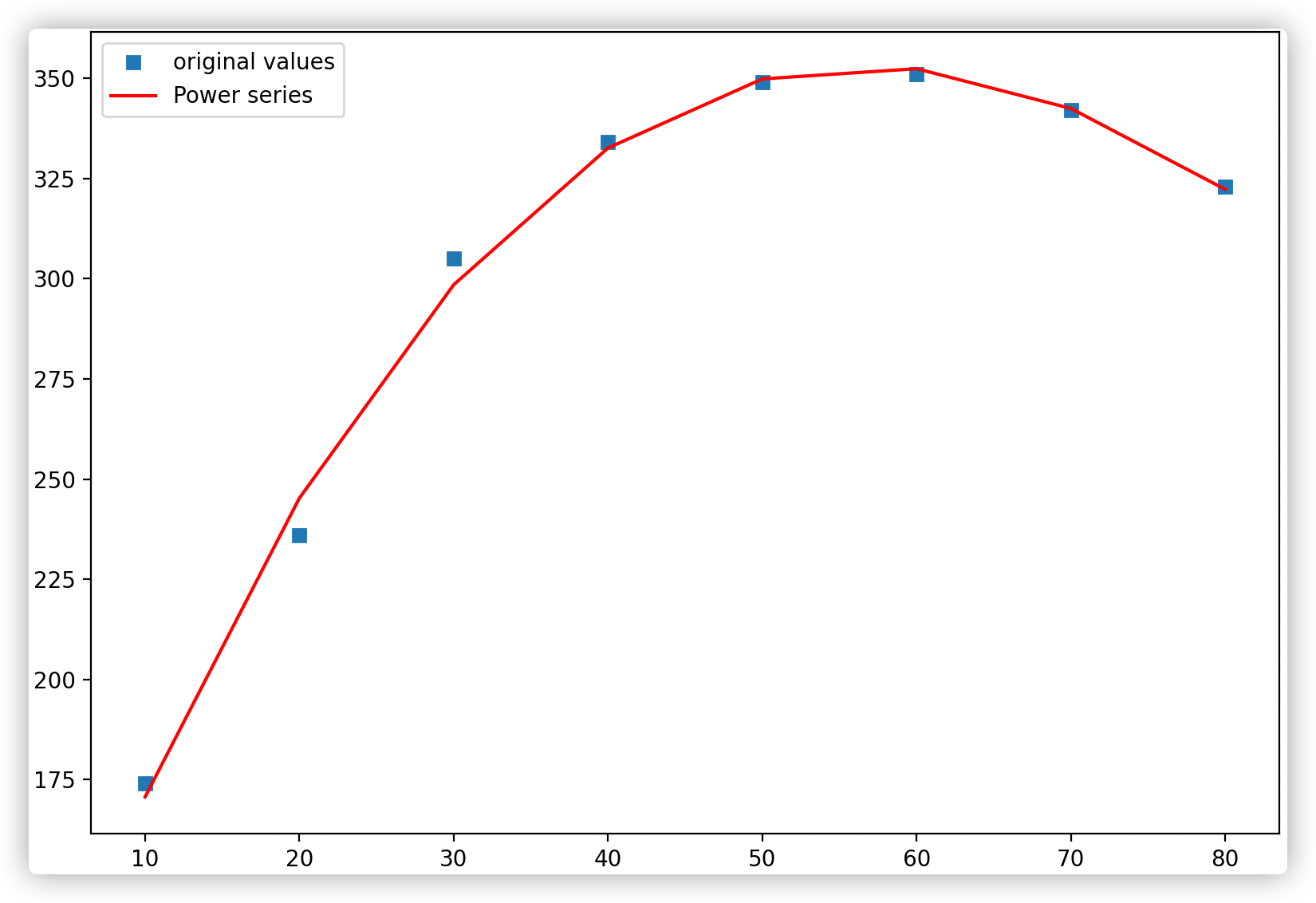
MARK
在官方文档会看到 Polynomial 这个类前面套了好几层numpy.polynomial.polynomial.Polynomial

实则关系是 numpy.polynomial 下面有个 polynomial.py 文件,文件里有个类是 Polynomial。同理,剩下五种多项式也是如此,chebyshev.py 有个 Chebyshev类
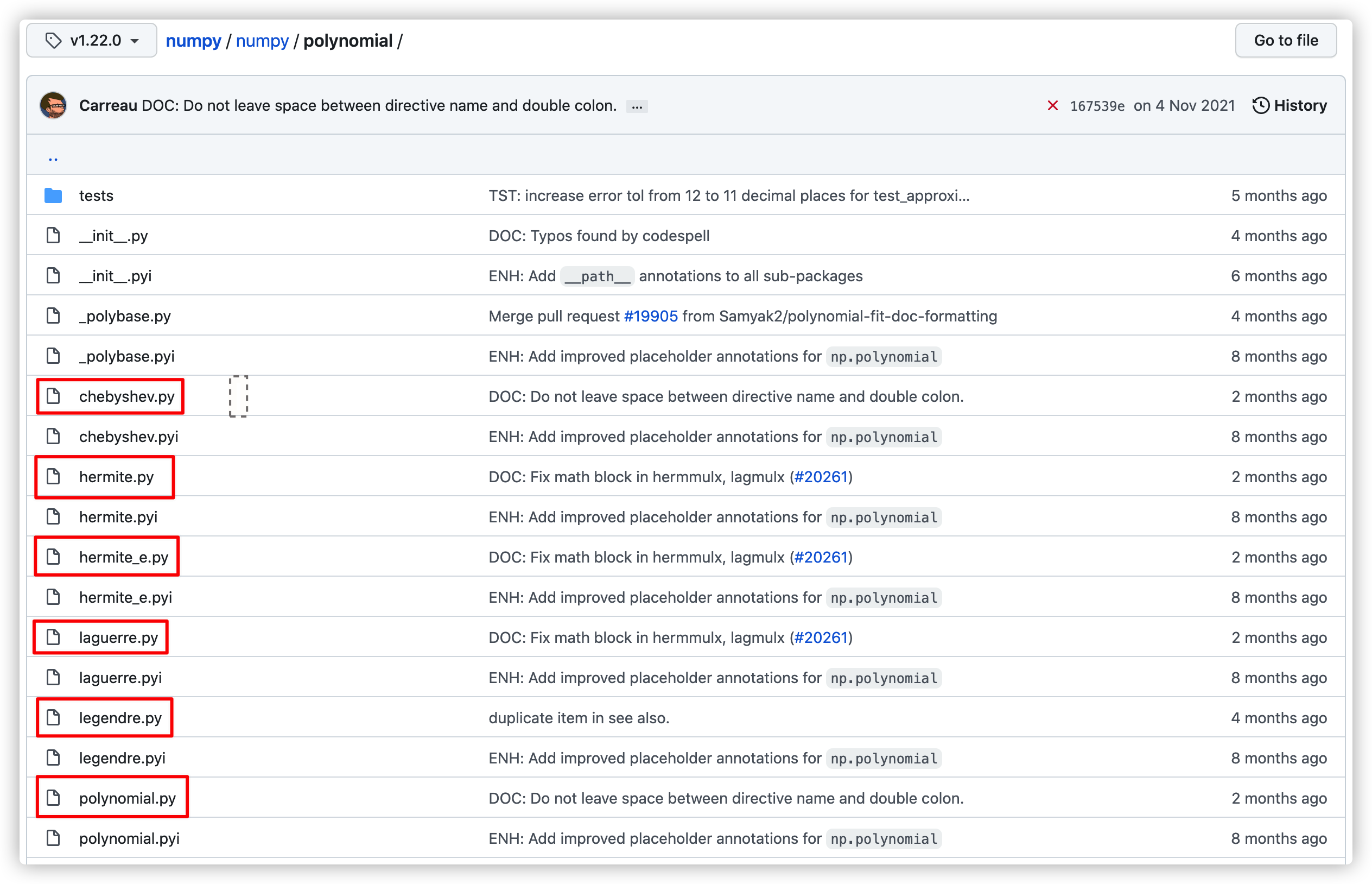
在实际使用的时候可以严格遵守这种关系
|
|
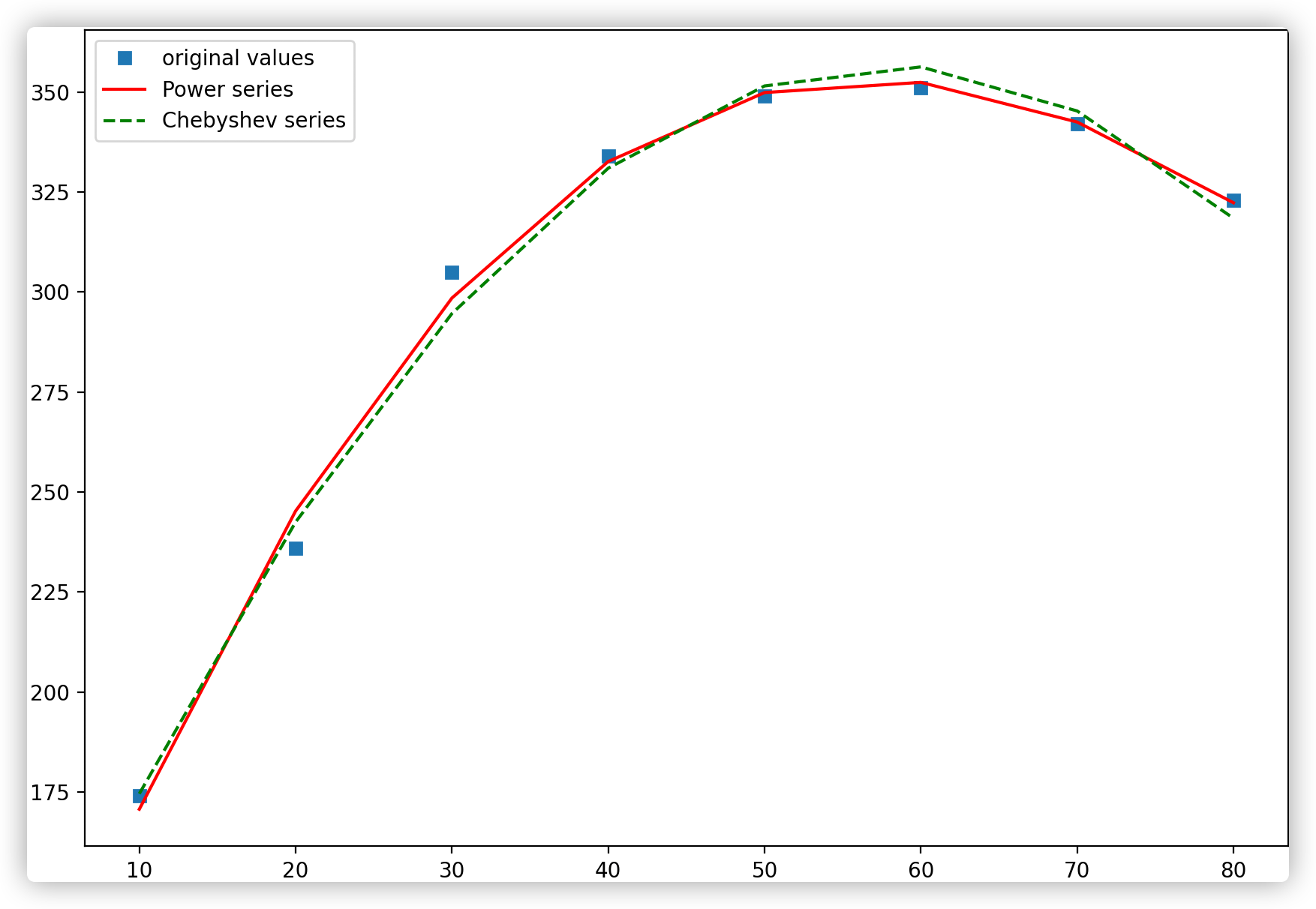
Reference
- https://numpy.org/doc/stable/reference/generated/numpy.log.html
- https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.curve_fit.html
- https://docs.python.org/3.7/library/math.html
- https://numpy.org/doc/stable/reference/routines.polynomials.html
- https://numpy.org/doc/stable/reference/routines.polynomials.package.html#module-numpy.polynomial
- https://numpy.org/doc/stable/reference/generated/numpy.polynomial.polynomial.polyfit.html#numpy.polynomial.polynomial.polyfit
- https://numpy.org/doc/stable/reference/routines.polynomials.html
- https://www.jianshu.com/p/44baeed131df
 胡子叔叔的小站
胡子叔叔的小站